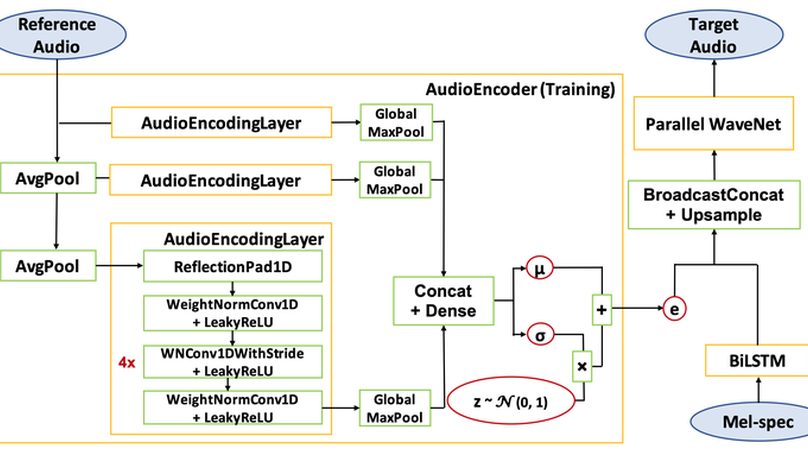
We present a universal neural vocoder based on Parallel WaveNet, with an additional conditioning network called Audio Encoder. Our universal vocoder offers real-time high-quality speech synthesis on a wide range of use cases. We tested it on 43 internal speakers of diverse age and gender, speaking 20 languages in 17 unique styles, of which 7 voices and 5 styles were not exposed during training. We show that the proposed universal vocoder significantly outperforms speaker-dependent vocoders overall. We also show that the proposed vocoder outperforms several existing neural vocoder architectures in terms of naturalness and universality. These findings are consistent when we further test on more than 300 open-source voices.

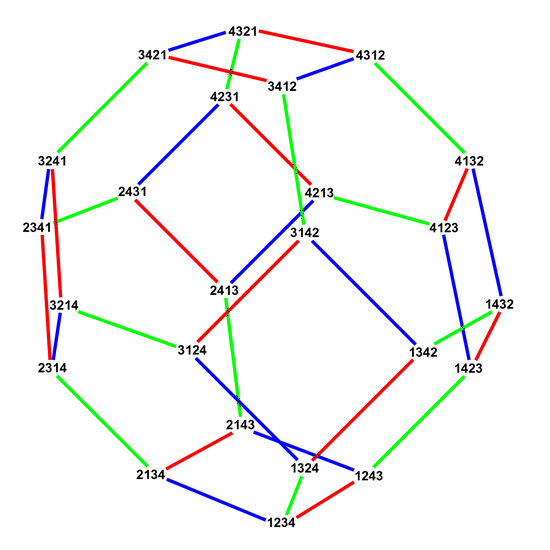
We show that the widely used Kendall tau correlation coefficient, and the related Mallows kernel, are positive definite kernels for permutations. They offer computationally attractive alternatives to more complex kernels on the symmetric group to learn from rankings, or learn to rank. We show how to extend these kernels to partial rankings, multivariate rankings and uncertain rankings. Examples are presented on how to formulate typical problems of learning from rankings such that they can be solved with state-of-the-art kernel algorithms. We demonstrate promising results on clustering heterogeneous rank data and high-dimensional classification problems in biomedical applications.